Design Theory

Factor of Safety

Although it uses ultimate limit state load factors/combinations, Tribli applies an additional factor of safety to all loads prior to being used in any of Tribli's design functions including; column, wall, pad footing, column transition and punching shear design. This value defaults to 1.20, but can be changed by the user in settings or by clicking on the text in the bottom right hand corner of the screen.

The value of the the design factor of safety can be changed to suit the level of detail of the model. The default value of 1.20 is appropriate for an early stage design where the final structural form is not yet locked in (initial column sizing for instance). Once the design has developed further, it may be appropriate to reduce the factor of safety provided the Tribli model is adequately detailed.

Design Codes

Although other codes are intended to be supported in future, Tribli currently only supports loading and design operations in accordance with Australian standards. Currently AS1170.1:2002 (live load reduction), AS1170.2:2021 (wind loads), AS1170.4:2007 (earthquake loads) and AS3600:2018 (concrete design) are used for load calculation and design purposes.

Columns

Columns are designed in accordance with AS3600:2018 section 10. The user shall bear in mind the following assumptions that are inherent in column designs performed by Tribli:

• All columns are assumed to be braced at their top and bottom levels, even if the column does not sit within the slab boundary at these levels
• Minimum column eccentricities are applied automatically. The user does not need to manually enter these into the column’s eccentricity fields
• Core confinement is checked according to the deemed to comply method outlined in Cl 10.7.3.4

Column effective lengths are calculated by taking the height between levels where columns within a given chain sit within the slab profile, adjusted for slab thicknesses and level offsets , then multiplying by the effective length ‘k’ factor specified for the column.

For design purposes, column eccentricities and moments are treated the same. The user-specified moment or eccentricity should be the larger of the applied moments at each end of the column. If required, the moment/eccentricity at the other end of the column may be specified using the ‘M1/M2’ factor defined for the column. Column moments/eccentricities shall be input according to the sign convention shown below.

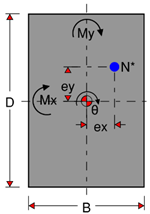
Column utilisations are usually reported as the ratio of the applied axial load to the maximum axial load that the column can sustain for a given applied moment/eccentricity, however if the biaxial bending of the column governs, it will be reported as the column utilisation instead.

Column fire checks are conducted using five methods; Table 5.6.3, Formula 5.6.3(2), Table 5.6.4, Table 5.7.2 (for blade columns) or the Annex C tables from EN1992-1-2. The column is said to pass fire checks if any of the five methods are satisfied. The EN1992-1-2 Annex C tables are used using the Ω and η factors as designated by AS3600.

Columns with their ‘Check as Wall’ parameter checked are checked in accordance with AS3600:2018 section 11.

Column shear checks are currently not supported.

Walls

Walls are designed in accordance with AS3600:2018 section 11. When designing walls, no check as made as to the validity if this design method, particularly in regard to the earthquake ductility class, soil class and overall wall H/L ratio. The user shall make an appropriate assessment of the validity of the section 11 method if relying on Tribli wall designs.

When assessing minimum horizontal reinforcement, Tribli uses the horizontal restraint and exposure class set for the particular wall, with the required degree of crack control being set in the global Tribli settings.

Wall effective lengths are calculated by taking the height between levels where walls within a given chain sit within the slab profile, adjusted for level offsets , then multiplying by the effective length ‘k’ factor specified for the wall. A wall is considered to be braced at a given level if at least 80% of the wall length sits within the slab outline. Unlike columns, wall effective lengths are not reduced by the slab thickness at their top-most level.

Currently, Tribli does not consider in-plane or out-of-plane moments in the design of walls. This means that the load on the wall is effectively averaged across the whole length of wall. For long walls this will very likely underestimate the peak stress in the walls caused by floor loads being applied unevenly to the wall. Therefore it is recommended that Tribli’s wall design module is only used for short walls, or walls that are very evenly loaded and that do not perform a stability function within the structure.

Pad Footings

Pad footings are designed as two-way slabs using bending theory in accordance with AS3600:2018 section 9. Depending on the dimensions of the pad, strut and tie in accordance with section 7 may be the correct method of analysis, and thus the method used by Tribli may not be appropriate. The user shall make an appropriate judgement on whether the bending theory results presented by Tribli are applicable to a given pad footing. Additionally, pads with a large aspect ratio (long and skinny) may not be reasonably be justified as two-way spanning elements and would thus need to be considered as one-way spanning. Tribli does not make this assessment automatically, and it is up to the user to determine the applicability of the two-way method used. The major implication of a one-way spanning element in regards to the design of pad footings is the applicability of clause 8.2.1.6 requiring minimum ligatures in slabs or beams greater than 750mm in depth.

In performing the design of pad footings the following checks are made; soil bearing stress, punching shear utilisation, beam shear utilisation and bending utilisation.

Soil bearing stress is checked by dividing the column working load by the area of the pad footing, then comparing to the user-defined max allowable soil bearing stress. If a footing concrete density of greater than zero is specified in the design settings, the weight of the footing will be added to the soil bearing stress.

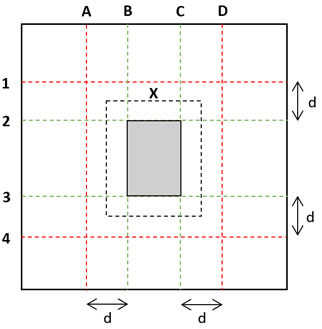
Punching shear checks are made in accordance with AS3600:2018 Cl 9.3.3. The punching shear perimeter ‘u’ is taken as the length of the line labelled ‘X’ in the diagram below. It is similar in shape to the column over, but offset by a distance of d_om/2 from the column face. The value of M*v is assumed to be zero for pad punching shear checks. The magnitude of the load assumed to be resisted by shear around the shear perimeter is equal to the ULS column load minus the portion of load that directly bears on the soil within the shear perimeter. The direct bearing component of the force is calculated by multiplying the ULS bearing pressure of the pad by the area enclosed by the shear perimeter ‘X’.

Beam shear is checked across the width of the pad footing in two directions, along the lines marked ‘A’/’D’ & ‘1’/’4’ in the diagram below. These lines represent the critical shear planes on either side of the column, and are generally assumed to sit at a distance ‘dv’ from the face of the column, though if the column and pad have incompatible rotations (they do not differ from each other by a factor of 90 degrees) then the shear is taken at a distance ‘dv’ from the pad centre. Shear is checked using the general method of Cl 8.2.4.2 with an assumed nominal max aggregate size of not less than 16mm. Shear reinforcement in pad footings is currently not supported.

Bending is checked across the width of the pad footing in two directions, along the lines marked ‘B’/’C’ & ‘2’/’3’ in the diagram below. These lines represent the critical bending planes on either side of the column, and taken at either 0.7a_sup from the column centre as per AS3600 Cl 6.2.3, or if the column and pad have incompatible rotations (they do not differ from each other by a factor of 90 degrees) then the moment is taken at the pad/column centre. An option is provided in the Tribli settings to ignore AS3600 Cl 6.2.3 and take the plane of maximum bending moment at the face of the column.

Self-weight of the pad footing is not used in any ULS pad footing checks.

By default, pads are checked using a plastic design method where the plan dimensions of the actual pad footing used for the analysis is reduced such that the soil bearing capacity is fully utilised. This pad represents a hypothetical pad-within-a-pad that would be the smallest and most efficient pad footing for a given column size and load. This approach should be used with caution for deep, shear governed pads as brittle shear failure may occcur before the assumed load redistribution is able to occur.

Raft Footings

Raft footings are spread footings that (unlike pad and strip footings) can support more than a single element (columns or walls). Conceptually they behave similarly to pad footings, however the design of rafts is usually more complex as the load is spread unevenly in the x and y directions due to either the shape of the raft or interaction of loads from the supported elements.

Tribli provides a basic plate element finite element method that allows for the calculation of settlements, bearing pressures and internal bending moments in rafts.

To complete the finite element analysis, first the raft geometry is meshed using either the Tribli internal meshing algorithm or an external plugin meshing algorithm. By default, the meshing algorithm will be selected automatically based on the geometry of the raft and supported elements, though this can be modified in the Tribli settings. The target mesh size is specified individually for each raft and can be modified in the raft properties dialog.

Compression-only springs elements are applied to each node of the finite element model based on the area of the plate elements connecting to the given node. The spring stiffness is calculated from the soil subgrade modulus specified by the user for each raft footing. The bending stiffness of the plate elements is constant for all plates (ie. no account is made for any non-linear stiffness behaviour of the raft) and is calculated from the thickness of the plates and the elastic modulus of the concrete (calculated internally based on the characteristic concrete compressive strength) before being factored down by the user-defined raft stiffness factor. The stiffness factor should be set by the user to a value that appropriately approximates the short and/or long term stiffness of the raft in bending. The shear modulus applied to the plate elements is calculated from the elastic modulus assuming a poissons ratio of 0.2, it is not reduced by the user-specified stiffness factor.

A raft is considered to be supporting any column or wall that sits entirely within the geometry of the raft (partially supported walls are ignored). The column or wall must also be the lowest element in its chain to be able to be supported by a raft. Supported elements are calculated automatically each time the raft analysis is performed. Column and wall loads are applied as node point-loads in the finite elements analysis, meaning that no account is taken of the bending stiffness of columns over, or of the in-plane stiffness of walls.

Raft bending moments reported by Tribli are given about the axis being considered. For example, the Mx moments are moments acting about the X axis, producing stresses in the top and bottom of the raft parallel to the Y axis. Positive moments are sagging moments, that is, moments that producing tension in bottom face of the raft. Inversely, negative moments are hogging moments, those producing tension in the top face of the raft.

Tribli can also complete approximate unreinforced punching shear checks for all columns supported by the rafts. Due to the larger depth of rafts when compared to slabs, punching shear perimeters can easily become deformed in rafts resulting in linear (or near-linear) critical shear planes. In such cases, the user should complete their own one-way (beam) shear checks to ensure the raft has adequate shear capacity for the applied loads.

Strip Footings

Strip footings are designed as one-way slabs using bending theory in accordance with AS3600:2018 section 9. Depending on the dimensions of the footing, strut and tie in accordance with section 7 may be the correct method of analysis, and thus the method used by Tribli may not be appropriate. The user shall make an appropriate judgement on whether the bending theory results presented by Tribli are applicable to a given strip footing.

In performing the design of strip footings, the following checks are made; soil bearing stress, shear utilisation and bending utilisation.

Tribli supports eccentric strip footings by calculating an elastic stress distribution across the width of the footing. The peak stress at the edge of the strip is used when assessing the overall bearing utilisation. If a footing concrete density of greater than zero is specified in the design settings, the weight of the footing will be added to the soil bearing stress.

Bending in the footing is checked at each face of the wall above and the bending utilisation at the most critical cross section is reported to the user. Note that for concentric strip footings (e=0), the bending utilisation each side of the wall will be identical.

Shear in the footing is assessed at a distance 'dv' each side of the wall face, with the concurrent moment also being calculated at this point. Tribli does not support the provision of shear reinforcement in strip footings, however the user should note that as the footing is designed as a one-way element it must be provided with shear ligatures where the depth of the footing exceeds 750mm as per AS3600 Cl 8.2.1.6. Tribli will flag this as a detailing error when the footing depth is greater than 750mm, however the unreinforced shear capacity of the footing will still be calculated and reported.

Self-weight of the footing is not used in any ULS strip footing checks.

Punching Shear

Tribli performs approximate column punching shear analyses to AS3600:2018 clause 9.3. By default moments transferred from the slab to the column (M*v) are taken to be equal to the defined Mx and My column moments. Column eccentricities are not considered in punching shear checks. The user should note the below assumptions made during punching shear checks:

• The slab depth is calculated at the centreline of the column only. No account is taken for any slab thickness reductions in the vicinity of the column
• dom is approximated by subtracting 40mm from the slab depth at the centreline of the column
• f’c is taken as the minimum concrete grade of any overlapping slabs
• The effective slab pre-stress is averaged across all overlapping slabs
• Equation 9.3.4(1) is used when calculating punching shear capacities with bending moments transferred from the slab. Capacities are checked in both primary directions.

The algorithm used to calculate the punching shear perimeter checks several possible critical shear perimeters and returns that which produces the smallest shear perimeter length. When viewing punching shear utilisations, a green line will be shown around the column indicating the critical shear perimeter used in the design. As the algorithm used to calculate the shear perimeter is not perfect, the user shall inspect all punching shear perimeters and validate that they are appropriate and correct.

Column Transitions

Tribli can perform approximate column transition checks. This function checks the bearing stress in the direct bearing zone between columns under and over at a given level and compares it to the effective (confined) concrete strength as calculated using AS3600:2018 clause 10.8. By default, Tribli will assume a small amount of load divergence by buffering the column overlap shape by some multiple of the slab thickness. This factor defaults to 0.5 times the slab thickness but can be changed in the settings menu. This buffer distance shall be used with caution, as even the default 0.5 d buffer distance may not be able to be justified with an appropriate strut & tie analysis as required by the code. By default, the edge condition of each column will be automatically calculated by searching for a slab edge within a given radius, however this can be modified individually for each column by setting the ‘Slab Restraint’ property of the column.

If the slab restraint condition is set to be calculated automatically, a circle will appear around the column (when viewing transition utilisations) indicating the slab edge search zone. If the circle falls entirely within the slab, the column is assumed to be ‘Interior’, if between 50% and 100% of the circle perimeter falls on the slab the column is assumed to be an ‘Edge’ column, if greater than 25% of the circle is on the slab the column is taken as ‘Corner’ otherwise no slab restraint is assumed.
A yellow shaded region shown when viewing transition utilisations indicates the direct bearing area between the column under and over.

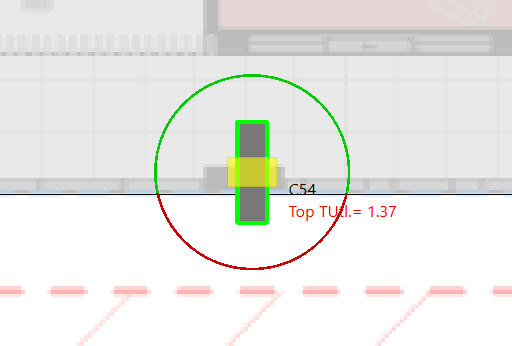
As with all Tribli design functions, the engineer shall take appropriate steps to validate all outputs produced.

Wind Loads

Tribli calculates wind loads according to AS1170.2:2021 for the eight major cardinal directions based on the parameters input by the user. Wind pressures are calculated at every level and applied to the exposed windward area of the structure in a given direction. The exposed windward area is calculated by multiplying the windward width of the slabs defined at the level by half the height to the level below, plus the windward width of the slabs defined at the level above multiplied by half the height to the level above. Were multiple slab regions exist at a given level, the exposed width of each component is summed to calculate the total exposed windward width (ie. No shielding is assumed to be provided by any slab region to any other).

The user should note the following:

• The load calculation does not currently assess the torsional loads generated by winds on tall buildings.
• The ‘Primary Structure’ and ‘Ultimate Loading’ parameters are applicable to regions B2, C & D only.
• The ‘Distance To Coast’ parameter is applicable to regions C & D only and is used to interpolate wind speeds between cyclonic regions, where maximum wind speeds are experienced at the coast and decrease as they move inland. The distance to the coast should always be less than 50km, with the one exception being the Pilbara region of Western Australia where, due to the existence of the D region, the C region may be further than 50km from the coast.
• The parameters ‘Terrain Category’, ‘Ms’, ‘Mt’, ‘Windward Cp,e’, ‘Leeward Cp,e’, ‘Ka’ and ‘Cdyn’ must be specified for each cardinal direction in the directions tab. Where ‘Windward Cp,e’ is positive and ‘Leeward Cp,e’ is negative (as should always be the case), ‘Kc’ is taken as 0.9, otherwise it is taken as 1.0. Directional factors are automatically applied based on the defined north point and wind region.
• The sign convention used in reporting shears and moments is as per the main Tribli interface, with positive X to the right, and positive Y towards the top of the screen. The right hand rule may be used to determine the direction of the bending moments about the X and Y axes.